顺序表示
顺序表示
定义
顺序表:顺序存储的线性表,是用一组地址连续的存储单元,依次存储线性表中的数据元素,使得在逻辑上相邻的两个元素在物理位置上也相邻。

顺序表中的元素的逻辑顺序与实际的物理位置相同
注意:
- 线性表中的元素的位序是从1开始的,例如1、2、3...
- 数组中的元素的下标是从0开始的,例如0、1、2...
# define MaxSize 20 // 定义常量MaxSize 用来声明顺序表的最大长度
// 线性表结构体定义【ElemType用来代指顺序表中元素的类型,例如高级语言中的int、string....】
typedef struct{
ElemType data[MaxSize]; // 顺序表的元素
int length; // 顺序表的长度
}SqList存储分配
静态分配:数组的大小和空间都是实现确定好的,一旦存储空间占满就会产生溢出,直接导致程序崩溃。(有点内存不够,宕机重启的意思....)
动态分配:存储数据的空间在程序执行过程中通过动态存储分配语句分配的,即便是数据空间占满,也可以另外开辟一块更大的空间,来替换原来的存储空间,满足扩充数据空间的目的。(有点动态规划的意思....)最重要的是:不需要像静态分配那样,一次性地固定线性表的空间和大小
#define InitSize 100 // 表长度初始化
// 动态分配数组顺序表的结构体定义
typedef struct{
ElemType *data; // 动态分配数组的指针
int MaxSize,length; // 数组的最大容量和当前元素个数
}SqList;动态分配语句
// C语言中
L.data=(ElemType*)malloc(sizeof(ElemType)*InitSize);
// C++ 中
L.data=new ElemType[InitSize];malloc()函数: 指针型函数,返回的指针指向该分配域的开头的位置。作用是在内存的动态存储区中分配一个长度为size的连续空间。百度百科
动态分配不是链式存储,而是属于顺序存储结构,动态分配的物理结构没有改变,依然是随机存取的方式。只是分配的空间大小可以在运行时决定;
顺序表的特点
- 随机访问【这是最主要的特点】,通过存储起始地址和元素序号O(1)时间内访问指定元素。
- 存储密度高,没有结点只存储数据元素,不像索引存储那样,还需要索引表什么的..
- 逻辑上相邻的元素物理上也相邻,插入和删除需要移动大量元素
基本操作
插入
在顺序表L的第i(1≤i≤L.length+1)个位置插入新的元素e
- 第一步:如果i非法,则直接返回false,插入失败,结束插入过程
- 第二步:i正常,将表的第i个元素以及后面的所有元素都向右移动一个位置,在腾出来的空位置插入元素e
- 第三步:顺序表插入成功,返回true
注意:先判空和临界值,提高算法健壮性
/*
* @Description: 顺序表的插入操作
* @Version: Beta1.0
* @Author: 微信公众号:储凡
* @Date: 2020-02-23 07:48:26
* @LastEditors: 微信公众号:储凡
* @LastEditTime: 2020-02-23 07:48:26
*/
bool ListInsert(SqList &L, int i, ElemType e){
// i非法 i=1 表头 i=L.length+1 表尾巴
if(i<1||i>L.length+1){
return false;
}
// 存储空间满,无法插入
if(L.length >= MaxSize){
return false;
}
// 遍历,将位置元素往后移动,注意从后往前循环,避免值被覆盖
for(int j=L.length; j>=i;j--){
L.data[j]=L.data[j-1];
}
// 此时,表L中的第i个元素和第i+1元素素值一样,将新元素存入i位置即可
// 第i个元素,对应的位置角标为i-1
L.data[i-1]=e;
// 表长度加1
L.length++;
// 返回插入成功
return true;
}注意:区别顺序表中的位序和角标;
时间复杂度
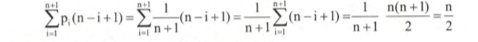
- 最好情况:在表尾插入,元素向后移动循环没有执行,时间复杂度O(1);
- 最坏情况:在表头插入,元素后移循环执行n次,时间复杂度为O(n);
- 平均情况:随机插入,平均次数为:n/2,对应的平均复杂度为O(n);
线性表插入算法的平均时间复杂度为:O(n)
Tips: 需要根据实现代码理解循环为什么是从后往前来实现元素后移,通过for循环可以很明显的看出表尾插入快,表头插入慢
删除
删除顺序表L中第i(1≤i≤L.length+1)个位置的元素
- 成功,返回true,将被删除的元素用引用变量返回;
- 失败,返回false
/*
* @Description: 顺序表的删除操作
* @Version: Beta1.0
* @Author: 微信公众号:储凡
* @Date: 2020-02-23 07:48:26
* @LastEditors: 微信公众号:储凡
* @LastEditTime: 2020-02-23 07:48:26
*/
bool ListDelete(SqList &L, int i, ElemType &e){
// i非法 i=1 表头 i=L.length+1 表尾巴
if(i<1||i>L.length+1){
return false;
}
// 存储空间满,无法插入
if(L.length >= MaxSize){
return false;
}
// 引用变量e赋值
e=L.data[i-1]
// 遍历,第i个元素后面的往前移动
for(int j=i; j<=L.length;j++){
// 从第i个元素开始,角标从i-1开始
L.data[j-1]=L.data[j];
}
// 此时,表L中的表尾元素和倒数第二个元素值一样,将表的长度-1
// 表长度减1
L.length--;
// 返回删除成功
return true;
}从这里来看,删除、插入元素都会涉及到大量的元素的移动(最好情况例外),总结而言:
- 元素从后往前移,循环从前往后遍历
- 元素从前往后移,循环从后往前遍历
时间复杂度:
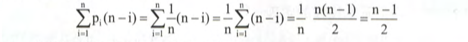
- 最好情况:删除表尾元素,不需要移动任何元素,时间复杂度为O(1);
- 最坏情况:删除表头元素,需要移动除第一个元素外的所有元素,时间复杂度为O(n);
- 平均情况:随机删除,平均需要(n-1)/2,对应的时间复杂度为O(n);
线性表删除算法的平均时间复杂度为O(n);
按值查找(顺序查找)
在顺序表L中查找第一个元素值等于e的元素,并返回位序
/*
* @Description: 顺序表的按值查找(顺序查找)
* @Version: Beta1.0
* @Author: 微信公众号:储凡
* @Date: 2020-02-23 07:48:26
* @LastEditors: 微信公众号:储凡
* @LastEditTime: 2020-02-23 07:48:26
*/
int LocateElem(SqList L,ElemType e){
int i;
// 循环判断
for(i=0;i<L.length;i++){
if(L.data[i]===e){
// i是元素的角标,i+1是具体元素的位序号
return i+1;
}
}
// 未命中,返回0,即:没有
return 0;
}注意理解位序的含义,即元素在线性表中的位置序号,角标为i(角标从0开始),对应的位序为i+1(位序从1开始)。当返回为0时,则直接代表没有命中;
时间复杂度:
- 最好情况:查找的元素在表头,只需要比较一次,循环成本最小,时间复杂度为O(1);
- 最坏情况:查找的元素在表尾或者不存在,需要完整遍历,比较n次,时间复杂度为O(n);
- 平均情况:随机查找表上的第i个(1≤i≤L.length)元素,平均次数为(n+1)/2,对应时间复杂度为O(n)
线性表按值查找(顺序查找)的平均时间复杂度为O(n);
顺序存取是读写方式,不是存储结构;顺序存储是存储结构,包括有:顺序存储、链式存储、索引存储、散列存储
